A matrix is a type of shorthand notation for systems of linear equations.
This includes systems of linear differential equations as well.
Matrices lead to very powerful and concise matrix equations that greatly simplify finding solutions to linear systems.
In this post, matrices and their basic operations are introduced but the connection to linear systems is left out.
Contents
Dimensions
An m x n matrix has m rows with n columns.
Each entry in the matrix is indexed with subscripts, first the row then the column.
2 x 2 matrix
\begin{bmatrix}
2 & 4 \\
3 & 1
\end{bmatrix}
3 x 2 matrix
\begin{bmatrix}
6 & 2 \\
1 & 5 \\
7 & 2
\end{bmatrix}
General m x n matrix
\begin{bmatrix}
x_{11} & x_{12} & x_{13} & \dots & x_{1n} \\
x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{m1} & x_{m2} & x_{m3} & \dots & x_{mn}
\end{bmatrix}
Algebra
Matrices follow the rules of matrix algebra.
Addition and Subtraction
Matrix addition works by adding together the elements at the same location in the two matrices.
$$
\begin{bmatrix}
2 & 4 \\
3 & 1
\end{bmatrix} +
\begin{bmatrix}
1 & 2 \\
2 & 3
\end{bmatrix}
=
\begin{bmatrix}
2+1 & 4+2 \\
3+2 & 1+3
\end{bmatrix}
=
\begin{bmatrix}
3 & 6 \\
5 & 4
\end{bmatrix}
$$
This only works when all matrices being added together have the same dimensions.
Addition is commutative where order does not matter.
$$A + B = B + A = C$$
Subtraction works the same way as addition.
$$
\begin{bmatrix}
2 & 4 \\
3 & 1
\end{bmatrix} –
\begin{bmatrix}
1 & 2 \\
2 & 3
\end{bmatrix}
=
\begin{bmatrix}
2-1 & 4-2 \\
3-2 & 1-3
\end{bmatrix}
=
\begin{bmatrix}
1 & 2 \\
1 & 2
\end{bmatrix}
$$
Multiplication
Multiplication is quite a bit more complicated.
We take the rows of the left-side matrix, and combine them with the columns of the right-side matrix.
You go across the row and down the column, multiplying the two numbers together and adding it all together as you go along.
See the example below:
$$
\begin{bmatrix}
2 & 4 \\
3 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 2 \\
2 & 3
\end{bmatrix}
=
\begin{bmatrix}
(2 \cdot 1) + (4 \cdot 2) & (2 \cdot 2) + (4 \cdot 3) \\
(3 \cdot 1) + (1 \cdot 2) & (3 \cdot 2) + (1 \cdot 3)
\end{bmatrix}
=
\begin{bmatrix}
10 & 16 \\
5 & 9
\end{bmatrix}
$$
You can see that the matrix is assembled based on the rows and columns, as highlighted below.
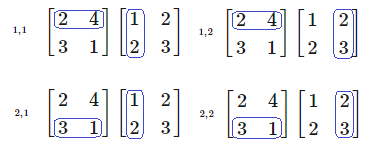
Unlike numbers, matrix multiplication is not commutative, meaning order matters!
$$AB \neq BA$$
The dimensions are very important when multiplying matrices.
The “inner” dimensions must be equal and the result uses the “outer” dimensions.
In the following example, a 2 x 3 matrix is multiplied by a 3 x 2 matrix which gives a 2 x 2 matrix.
$$
\begin{bmatrix}
1 & 2 & 3 \\
9 & 8 & 7
\end{bmatrix}
\begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6
\end{bmatrix}
$$
$$
=
\begin{bmatrix}
(1 \cdot 1) + (2 \cdot 3) + (3 \cdot 5) & (1 \cdot 2) + (2 \cdot 4) + (3 \cdot 6) \\
(9 \cdot 1) + (8 \cdot 3) + (7 \cdot 5) & (9 \cdot 2) + (8 \cdot 4) + (7 \cdot 6)
\end{bmatrix}
$$
$$
=
\begin{bmatrix}
22 & 28 \\
68 & 92
\end{bmatrix}
$$
In general, the dimensions follow the rule :
$$(m, n) \times (n, p) = (m, p)$$
Row Operations
To be completed…